向 Matrix67 致敬，我也来写点科普文章。

假期给初一、初二小孩讲几何课的时候，都提到了下面的命题：四边形 $ABCD$中， $E,F$依次是边 $BC$上的两个三等分点， $G,H$依次是边 $AD$上两个三等分点，求证 $S_{ABCD}=3S_{EFHG}$。

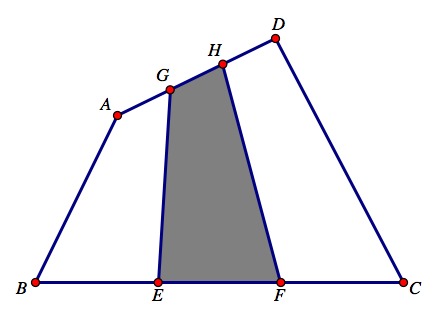
这道题目立即让我联想起了张景中院士的一本科普书，上课的时候我记不得这本书的名字了，后来回去搜索了一下，叫《新概念几何》。我的爸妈一般不给我买书（可能是因为买过两套四大名著我都不看的关系吧），记忆中他们还给我买过的书只有《十万个为什么（小学版）》和《新概念几何》了。

在《新概念几何》中提到过一个问题，叫做井田问题：传说从前的农民要分地的话，没有很精准的丈量工具，也不懂几何或是微积分，所以都采取一些近似的方法。有一天，村里的九户人家发现了一块四边形的田地，他们打算平分这块田。于是他们通过脚步丈量四条边后，将四边都三等分后，如下图将田分为了九块。

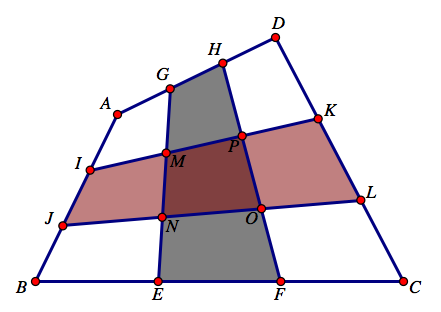
很明显，这块田地没有被九等分。但会不会像之前的“三分田地”问题一样，有类似的结论呢？很自然的一个猜测是最中间的土地面积是总面积的九分之一。其数学表述如下：四边形 $ABCD$中， $E,F$依次是边 $BC$上的两个三等分点， $G,H$依次是边 $AD$上两个三等分点， $I,J$依次是边 $AB$上的两个三等分点， $K,L$依次是边 $DC$上两个三等分点，求证 $S_{ABCD}=9S_{MNOP}$。

由于整个问题犹如在一块田中写一个井字，井田问题由此得来。

记得当时上课的时候，由于是即兴想到这个问题，双核同时运转，只顾着把故事编得生动一些，没腾出脑子去想解答，所以留下这个问题让小朋友自己回家思考了……

实际上，建立在之前的三分田地的结论上，这个问题是很容易解决的：

由之前的结论，红色四边形 $IJLK$的面积是整个面积的三分之一。假设我们能再证明 $M,P$和 $N,O$分别是 $IK, JL$的三等分点，那再次利用三分田地的结论，我们就能证明红黑相交的部分 $MPNO$的面积是红色四边形 $IJLK$的三分之一，也就是原四边形的九分之一了。

最后我们证明 $M,P$和 $N,O$确实分别是 $IK, JL$的三等分点，为此我们只证明 $M$是 $IK$的三等分点。

为了能看得更清楚，我们考虑与需要证明的结论有关的部分。

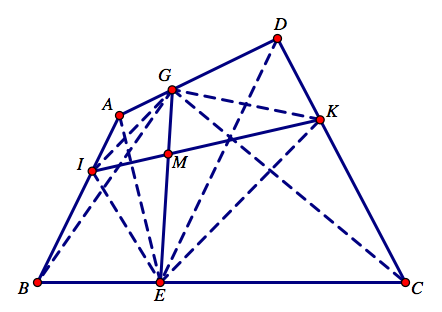
由定比分点公式，我们有关于面积的等式：

于是 $KM = 2IM$，就证明了需要的结论。

通过类似的论证，读者还能将井田问题中的三等分替换为五等分、七等分甚至任意 $2n+1$等分。进行类似的面积划分后，最中间那块的面积便是 $(2n+1)^2$分之一了。