In this exposition, we explore the behavior of the Hardy–Littlewood maximal function of measures that are singular with respect to Lebesgue measure.

We are going to prove that for every positive Borel measure $s$ that is singular with respect to Lebesgue measure $m$,

for all $h >s(\mathbb{T})$, where $\mathbb{T}=\mathbb{R}/\mathbb{Z}$ is a torus and $M_s$ is the Hardy–Littilewood maximal function of the measure $s$ defined by

where the supreme is over all the balls containing the point $x$ in the torus.

Yue Pu told me this problem a couple of days ago. Though I don’t feel confident solving analysis problems, I wanted to see how much I have learnt from Giovanni Leoni. Finally, after staring at the problem for about 6 hours, Yue and I came up with an answer. The proof is modified from Yue’s write-up.

For experts among the readers, our first step is to exploit Calderón–Zygmund covering lemma. We will explain this in detail.

Since two measures $m$ and $s$ are mutually singular, there exist two disjoint sets $M$ and $S$ whose union is $\mathbb{T}$ such that $s(M)=m(S)=0$. In other words, $m$ lives in $M$ and $s$ lives in $S$.

Let $A$ be the set of all atoms of $s$, i.e., $A=\{x: s(x) >0\}\subset\mathbb{T}$. Define $E(x):=\{x+\frac{m}{2^n}: m,n\in\mathbb{N}\}\subset\mathbb{T}$ for all $x\in\mathbb{T}$, where the addition is under mod $1$. Note that $A$ and $E(x)$ are both countable, so there exists $e\in\mathbb{T}$ such that $A\cap E(e)=\emptyset$. Without loss of generality, we may assume $e=0$ because we may choose a suitable point on the torus as $0$. We abbreviate $E(0)$ by $E$ which is going to be the set of the endpoints of some intervals.

Fix $h >s(\mathbb{T})$. Now we are ready to apply the Calderón-Zygmund decomposition according to the height $h$.

We can chop the torus into two disjoint intervals $(0, 1/2)$ and $(1/2, 1)$ both of length $1/2$. Notice that at most one of them, denoted as $I_1$ if any, whose average, namely $s(I_1)/m(I_1)$, is greater than or equal to $h$. Since $s(\mathbb{T})< h$, we get an upper bound for the average of $I_1$, $h\leq s(I_1)/m(I_1) ds < 2h$.

We can keep chopping those intervals whose average is less than $h$ into half and pick out sub-intervals whose average is no less than $h$. Inductively, we can generate an enumerable sequence of mutually disjoint open intervals $\{I_n\}$, each satisfying $h \leq s(I_n)/m(I_n) < 2h$, which implies $s(I_n)< 2hm(I_n)$.

Let $I=\bigcup_n{I_n}$. We claim that $s(I)=s(\mathbb{T})$. If this is the case, then

Left to prove the claim. To prove $s(I)=s(\mathbb{T})$, we only need to show $s(S-I)=0$ as $s$ lives in $S$. Note that $s(E)=0$ since $A$, the set of the atoms of $s$, is disjoint from $E$ and $E$ is countable. It suffices to show $s(S-I-E)=0$.

Let $K$ be a compact set contained in $S-I-E$. Since for a positive Borel measure, one can always approximate a Borel set from inside by compact sets, it is enough to show $s(K)=0$.

For any $\epsilon >0$, as $m(S)=0$, we may choose an open set $U$ such that $S\subset U$ and $m(U)< \epsilon$. We want to show for all $x$ in $K\subset S-I-E$, we can always find two intervals $J_x$ and $J_x^+$ both containing $x$ such that $4m(J_x)=m(J_x^+)$, $s(J_x^+)< hm(J_x^+)$ and $3J_x\subset J_x^+\subset U$, where $3J$ denotes the open interval that has the same center as $J$ but three times the radius.

According to the decomposition process, we can find an infinite sequence of descending open intervals $\{J_n\}_{n=1}^\infty$ containing $x$ such that $J_{n+1}$ is the left or right half of $J_n$ and $s(J_n)< hm(J_n)$ for all $n$. This is possible because $x\notin I\cup E$. Note that $x$ cannot always lie in the left half of $J_n$ for all sufficiently large $n$ and similarly $x$ cannot always lies in the right half of $J_n$ for all sufficiently large $n$. In other words, for infinitely many times, $J_{n+2}$ is the right half of $J_{n+1}$ which is the left half of $J_{n}$.

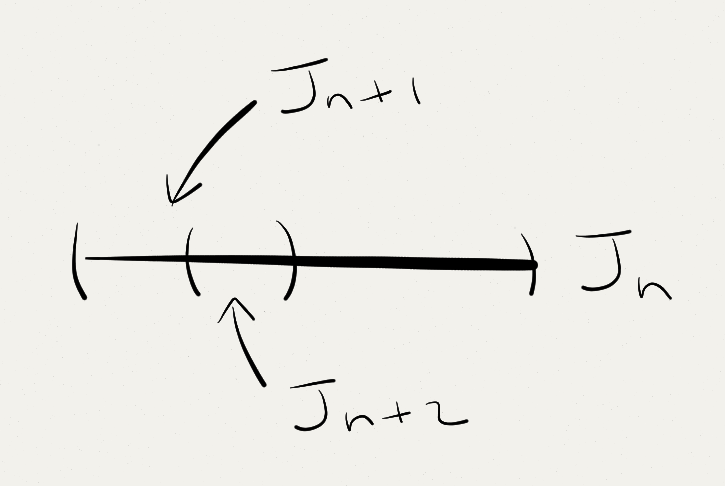
Therefore we can always find sufficiently large $n$ such that $J_n\subset U$. Now for every $x\in K\subset U$, there exist $J_x$ which is $J_{n+2}$ above, and $J_x^+$ which is $J_n$ above such that $x\in J_x$, $3J_x\subset J_x^+\subset U$, $m(J_x^+)=4m(J_x)$, and $s(J_x^+)< hm(J_x^+)$. Hence $\{J_x\}_{x\in K}$ is an open cover of the compact set $K$. We can choose a finite sub-cover, pass it to Vitali covering lemma and spit out a sub-collection $\{J_{x_n}\}_{n=1}^N$ which are disjoint balls such that $K\subset\bigcup_{n=1}^N 3J_{x_n}$. Now we have

As $\epsilon >0$ is chosen arbitrarily, we have $s(K)=0$, which yields the claim.

Remark. The fact that $s(\mathbb{T})< \infty$ which is implicitly required in the problem is used to prove the countability of $A$, the set of all atoms of $s$.

Remark. I have no idea whether the result is sharp in terms of the constant multiplier on the right hand side of the inequality.