Notations.

1. $\mathbb{N}$ – the set of natural numbers;
2. $\binom{M}{k}$ – the family of all subsets of $M$ of size $k$;
3. $\binom{M}{< \omega}$ – the family of all finite subsets of $M$;
4. $\binom{M}{\omega}$ – the family of all infinite subsets of $M$;

The infinite Ramsey theorem, in its simplest form, states that for every partition $\binom{\mathbb{N}}{k} = \mathcal{F}_1 \sqcup \dots \sqcup \mathcal{F}_r$, there exists an infinite set $M\subset \mathbb{N}$ such that $\binom{M}{k}\subset \mathcal{F}_i$ for some $i\in [r]$. The Nash-Williams‘ partition theorem can be seen as a strengthening of the infinite Ramsey theorem, which considers a partition of a subset of $\binom{\mathbb{N}}{< \omega}$.

Notations.

1. $\mathcal{F}\restriction M$ – $\mathcal{F}\cap 2^M$, that is, the set $\{s\in\mathcal{F} : s\subset M\}$.
2. $s \sqsubset t$, where $s,t$ are subsets of $\mathbb{N}$ – $s$ is an initial segment of $t$, that is $s = \{n\in t : n \le \max s\}$.

Definition. Let set $\mathcal{F} \subset \binom{\mathbb{N}}{< \omega}$.

1. $\mathcal{F}$ is Ramsey if for every partition $\mathcal{F}=\mathcal{F}_1\sqcup \dots\sqcup\mathcal{F}_r$ and every $M\in\binom{\mathbb{N}}{\omega}$, there is $N\in\binom{M}{\omega}$ such that $\mathcal{F}_i\restriction N = \emptyset$ for all but at most one $i\in[r]$.
2. $\mathcal{F}$ is a Nash-Williams family if for all $s, t\in\mathcal{F}, s\sqsubset t \implies s = t$.

Theorem (Nash-Williams 1965). Every Nash-Williams family is Ramsey.

The proof presented here is based on the proof given by Prof. James Cummings in his Infinite Ramsey Theory class. The purpose of this rewrite is to have a proof that resembles the one of the infinite Ramsey theorem.

Notation. Let $s\in\binom{\mathbb{N}}{< \omega}$ and $M\in\binom{\mathbb{N}}{\omega}$. Denote

Definition. Fix $\mathcal{F}\subset \binom{\mathbb{N}}{< \omega}$ and $s\in \binom{\mathbb{N}}{< \omega}$.

1. $M$ accepts $s$ if $[s, M]\cap \mathcal{F}\neq \emptyset$ and $M$ rejects $s$ otherwise;
2. $M$ strongly accepts $s$ if every infinite subset of $M$ accepts $s$;
3. $M$ decides $s$ if $M$ either rejects $s$ or strongly accepts it.

We list some properties that encapsulates the combinatorial characteristics of the definitions above.

Properties.

1. If $M$ decides (or strongly accepts, or rejects) $s$ and $N\subset M$, then $N$ decides (respectively strongly accepts, rejects) $s$ as well.
2. For every $M\in\binom{\mathbb{N}}{\omega}$ and $s\in\binom{\mathbb{N}}{< \omega}$, there is $N_1\in\binom{M}{\omega}$ deciding $s$. Consequently, there is $N_2\in\binom{M}{\omega}$ deciding every subset of $s$.

Proof of Theorem. Enough to show that if $\mathcal{F} = \mathcal{F}_1\sqcup \mathcal{F}_2$, then for every $M\in\binom{\mathbb{N}}{\omega}$, there is infinite $N\in \binom{M}{\omega}$ such that $F_i \restriction N = \emptyset$ for some $i\in[2]$.

We are going to use $\mathcal{F}_1$ instead of $\mathcal{F}$ in the definitions of “accept”, “reject”, “strongly accept” and “decide”. Find $N\in \binom{M}{\omega}$ that decides $\emptyset$. If $N$ rejects $\emptyset$, by definition $\mathcal{F}_1\restriction N = [\emptyset, N]\cap \mathcal{F}_1 = \emptyset$. Otherwise $N$ strongly accepts $\emptyset$.

Inductively, we build a decreasing sequence of infinite sets $N \supset N_1 \supset N_2\supset \dots$, an increasing sequence of natural numbers $n_1, n_2, \dots$, and maintain that $n_i\in N_i, n_i < \min N_{i+1}$ and that $N_i$ strongly accepts every $s\subset \{n_j : j < i\}$. Initially, we take $N_1 = N$ as $N$ strongly accepts $\emptyset$.

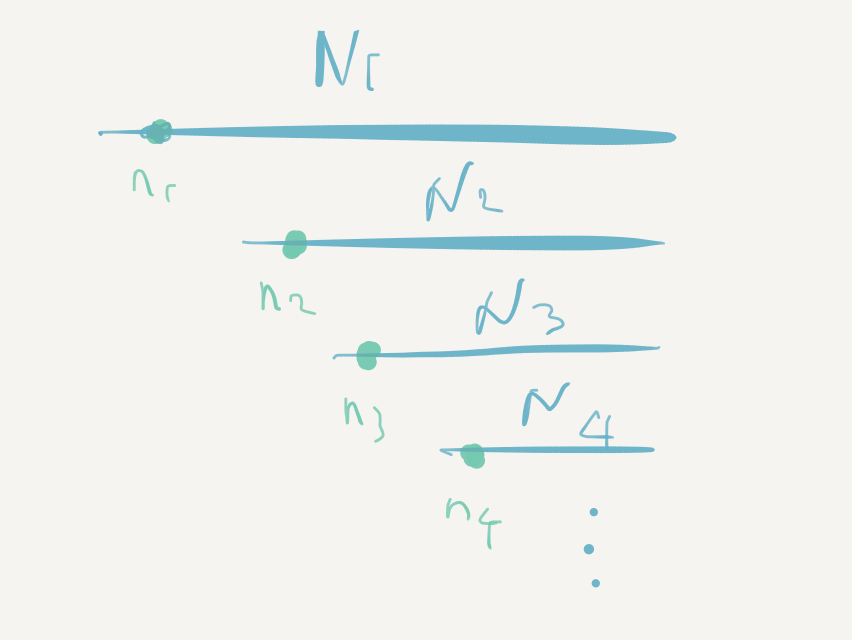
Suppose $N_1 \supset \dots \supset N_i$ and $n_1 < \dots < n_{i-1}$ have been constructed. In the following lemma, when taking $M = N_i$ and $s = \{n_j : j < i\}$, it spits out $m$ and $N$, which are exactly what we need for $n_i$ and $N_{i+1}$ to finish the inductive step.

Lemma. Suppose $M\in\binom{\mathbb{N}}{\omega}$, $s\in\binom{\mathbb{N}}{< \omega}$ and $\max s < \min M$. If $M$ strongly accepts every subset of $s$, then there are $m \in M$ and $N \in \binom{M}{\omega}$ such that $n < \min N$ and $N$ strongly accepts every subset of $s\cup \{n\}$

Proof of lemma. We can build $M = M_0 \supset M_1\supset M_2 \supset \dots$ such that for every $i$, $m_i := \min M_i < \min M_{i+1}$ and $M_{i+1}$ decides every subset of $s\cup \{m_i\}$. It might happen that $M_{i+1}$ rejects a subset of $s\cup \{m_i\}$. However, we claim that this cannot happen for infinitely many times.

Otherwise, by the pigeonhole principle, there is $t\subset s$ such that $I = \{i : M_{i+1} \text{ rejects }t\cup\{m_{i}\}\}$ is infinite. Let $M' = \{m_i : i\in I\}$. Note that $[t, M'] \subset \cup_i [t\cup\{m_i\}, M_{i+1}]$, and so $[t,M']\cap \mathcal{F}_1\subset \cup_i \left([t\cup\{m_i\}, M_{i+1}]\cap\mathcal{F}_1\right) = \emptyset$. Hence $M'\subset M$ rejects $t\subset s$, which is a contradiction.

Now we pick one $i$ such that $M_{i+1}$ strongly accepts every subset of $s\cup\{m_i\}$, and it is easy to check that $m = m_i$ and $N = M_{i+1}$ suffice. □

Finally, we take $N_\infty = \{n_1, n_2, \dots\}$. For any $s\in\binom{N_\infty}{< \omega}$, there is $i$ such that $s\subset \{n_1, \dots, n_{i-1}\}$. Note that $N_i$ strongly accepts $s$ and $N_\infty\subset N_i$. Therefore $N_\infty$ (strongly) accepts $s$, that is $[s, N_\infty]\cap \mathcal{F}_1 \neq \emptyset$, and say $t\in [s, N_\infty]\cap \mathcal{F}_1$. Because $t\in\mathcal{F}_1$ and $\mathcal{F} = \mathcal{F}_1 \sqcup \mathcal{F}_2$ is a Nash-Williams family, $s\notin \mathcal{F}_2$. □