Here is a problem from Week of Code 29 hosted by Hackerrank.

Problem. Given two integers $q_1$ and $q_2$ ($1\le q_1 \le q_2 \le 10^{15}$), find and print a common fraction $p/q$ such that $q_1 \le q \le q_2$ and $\left|p/q-\pi\right|$ is minimal. If there are several fractions having minimal distance to $\pi$, choose the one with the smallest denominator.

Note that checking all possible denominators does not work as iterating for $10^{15}$ times would exceed the time limit (2 seconds for C or 10 seconds for Ruby).

The problem setter suggested the following algorithm in the editorial of the problem:

1. Given $q$, it is easy to compute $p$ such that $r(q) := p/q$ is the closest rational to $\pi$ among all rationals with denominator $q$.
2. Find the semiconvergents of the continued fraction of $\pi$ with denominators $\le 10^{15}$.
3. Start from $q = q_1$, and at each step increase $q$ by the smallest denominator $d$ of a semiconvergent such that $r(q+d)$ is closer to $\pi$ than $r(q)$. Repeat until $q$ exceeds $q_2$.

Given $q$, let $d = d(q)$ be the smallest increment to the denominator $q$ such that $r(q+d)$ is closer to $\pi$ than $r(q)$. To justify the algorithm, one needs to prove the $d$ is the denominator of one of the semiconvergents. The problem setter admits that he does not have a formal proof.

Inspired by the problem setter’s approach, here is a complete solution to the problem. Note that $\pi$ should not be special in this problem, and can be replaced by any other irrational number $\theta$. Without loss of generality, we may assume that $\theta\in(0,1)$.

We first introduce the Farey intervals of $\theta$.

1. Start with the interval $(0/1, 1/1)$.
2. Suppose the last interval is $(a/b, c/d)$. Cut it by the mediant of $a/b$ and $c/d$ and choose one of the intervals $(a/b, (a+c)/(b+d)), ((a+c)/(b+d), c/d)$ that contains $\theta$ as the next interval.

We call the intervals appeared in the above process Farey intervals of $\theta$. For example, take $\theta = \pi - 3 = 0.1415926...$. The Farey intervals are:

The Farey sequence of order $n$, denoted by $F_n$, is the sequence of completely reduced fractions between 0 and 1 which when in lowest terms have denominators less than or equal to $n$, arranged in order of increasing size. Fractions which are neighboring terms in any Farey sequence are known as a Farey pair. For example, Farey sequence of order 5 is

Using the Stern–Brocot tree, one can prove that

Lemma 1. For every Farey interval $(a/b, c/d)$ of $\theta$, the pair $(a/b, c/d)$ is a Farey pair. Conversely, for every Farey pair $(a/b, c/d)$, if $\theta \in (a/b, c/d)$, then $(a/b, c/d)$ is a Farey interval.

We say $p/q$ is a good rational approximation of $\theta$ if every rational between $p/q$ and $\theta$ (exclusive) has a denominator greater than $q$.

By the definition of Farey sequence, incorporating with Lemma 1, we know that

Lemma 2. A rational is an endpoint of a Farey interval of $\theta$ if and only if it is a good rational approximation of $\theta$.

In fact, one can show that the endpoints of Farey intervals and semiconvergents of continued fraction are the same thing! Thereof, the problem setter’s claim follows immediately from:

Proposition. Given $q$, let $r(q) = p / q$ be the rational closest to $\theta$ with denominator $q$. If $d = d(q)$ is the minimal increment to $q$ such that $r(q + d) = (p + c) / (q + d)$ is closer to $\theta$ than $r(q)$, then $c/d$ is a good rational approximation.

Remark. The proposition states that the increments to $p/q$ always come from a good rational approximation. It is stronger than the problem setter’s statement, which only asserts that the increment to the $q$ comes from a good rational approximation.

Proof. In $(x, y)$-plane, plot the trapezoid defined by

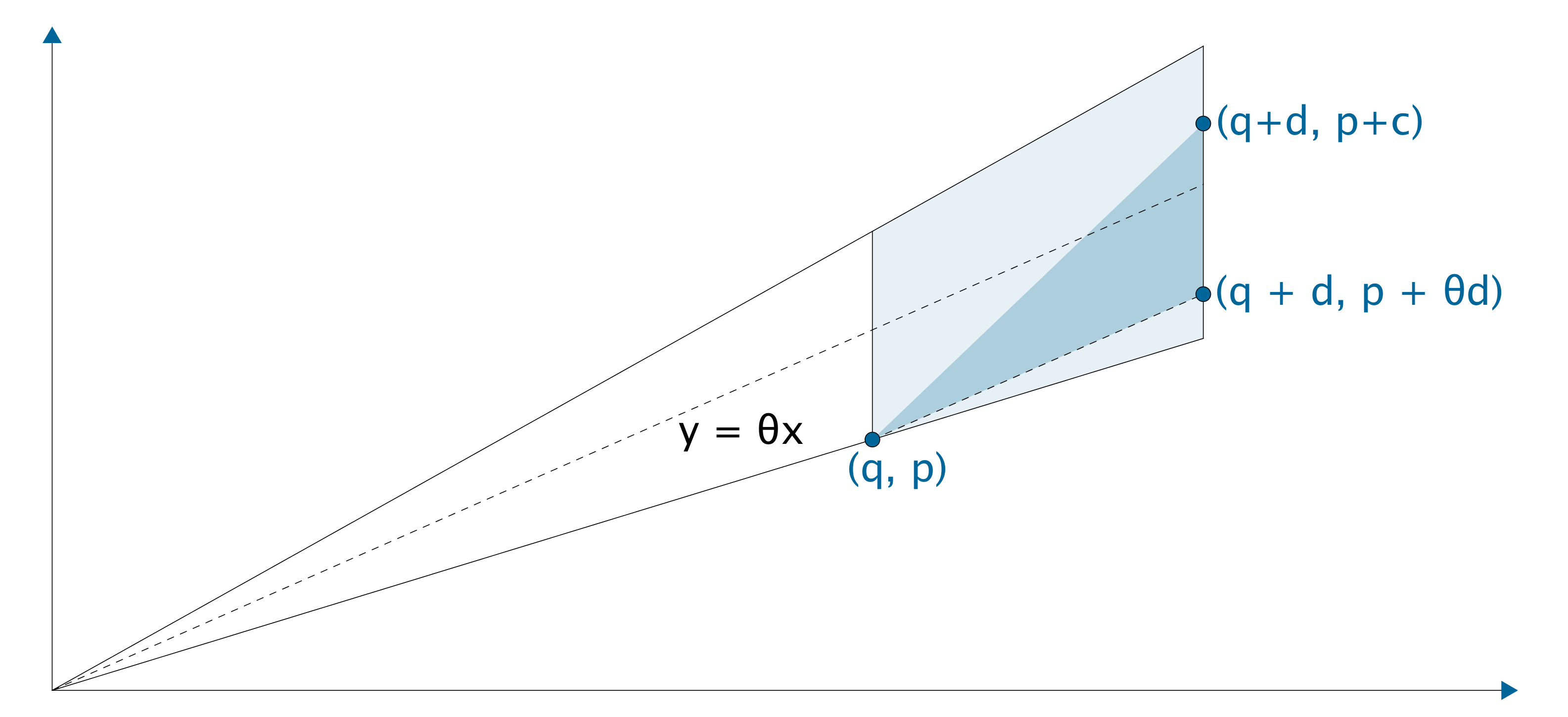
Also we interpret rational numbers $p/q, (p+c)/(q+d)$ as points $A = (q, p), B = (q+d, p+c)$. Let the line through $(q, p)$ parallel to $y=\theta x$ intersect the vertical line $x = q+d$ at $C = (q+d, p+\theta d)$. By the definition of $d$, we know that the trapezoid does not contain lattice points. In particular, there is no lattice point in the interior of the triangle $ABC$. In the coordinate system with origin at $A$, $B$ has coordinate $(d, c)$ and the line through $A, C$ is $y = \theta x$. Since triangle $ABC$ contains no lattice points, there is no $(b, a)$ with $b < d$ such that $a/b$ is between $\theta$ and $c/d$. In other words, $c/d$ is a good rational approximation. □

Here is a fine print of the algorithm. Because floats may not have enough precision for the purpose of computation, we will instead use a convergent of the continuous fraction of $\pi$ instead. All the computations will then happen in $\mathbb{Q}$. Finally, we present the algorithm.

P = Rational(5706674932067741, 1816491048114374) - 3
# find endpoints of Farey intervals
a, b, c, d = 0, 1, 1, 1
farey = [[a,b],[c,d]]
while (f = b + d) <= max - min
  farey << [e = a + c, f]
  if P < Rational(e, f)
    c, d = e, f
  else
    a, b = e, f
  end
end
min, max = gets.split.map(&:to_i)
p_min = (P * q).round
# increase p_min/min by frations in farey
while min <= max
  c, d = nil, nil
  farey.each do |a, b|
    break if min + b > max
    if (Rational(p_min + a, min + b) - P).abs < (Rational(p_min, min) - P).abs
      c, d = a, b
      break
    end
  end
  break if d == nil
  p_min += c; min += d
end
puts "#{p_min + 3 * min}/#{min}"