Binomial numbers and binomial theorem
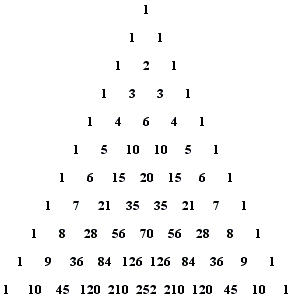
Definition The kth number in the nth row of the Pascal triangle is denoted by {n \choose k}. Careful! The top row is the 0th row, the leftmost numbers are the 0th numbers in the rows.
Theorem [Binomial Theorem] (a+b)^n = {n \choose 0} a^nb^0 + {n \choose 1} a^{n-1}b^1 + {n\choose 2} a^{n-2}b^2 + \dots + {n \choose n} a^0b^n.
Example Expand (1+x)^n and (1-x)^n.
Definition Factorial of n is denoted by n! := 1 x 2 x … x n. Convention: 0! = 1. Fact {n\choose k} = \frac{n!}{k!(n-1)!}.
Further reading Pascal’s pyramid and trinomial expansion.
One-to-one, onto, and bounded functions
Definition (one-to-one) A function f\colon A\to B is one-to-one if for every x_1, x_2 \in A, x_1 \neq x_2 implies f(x_1) \neq f(x_2).
Definition (onto) A function f\colon A\to B is onto if for every y\in B there exists x\in A such that f(x) = y.
Definition (bounded) A function f\colon A\to B is bounded if there exists M \in \mathbb{R} such that for all x\in A, -M \le f(x)\le M.
Examples Function f\colon \mathbb{R} \to \mathbb{R} defined by f(x) = x^3 is both one-to-one and onto, but it is not bounded. However f(x) = \sin x is bounded.
Riddle Find a one-to-one function f\colon \mathbb{R}\to \{\text{irrational numbers}\}.
Graphs of trig function
Graphs of sine, cosine and tangent functions.
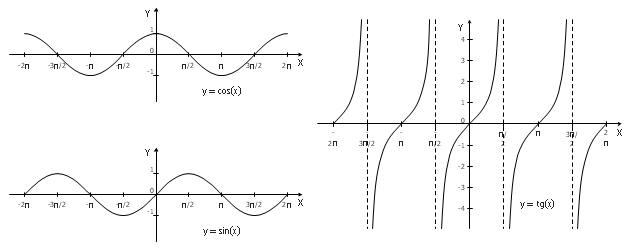
Periodicity of sine and cosine is 2\pi, and the periodicity of tangent is \pi. Sine and cosine functions are bounded, whereas tangent is not bounded.
List of trig formulas
Try to memorize the following basic formulas:
- \cos^2 \alpha + \sin^2 \alpha = 1^2.
- \sin (\pi / 2 - \alpha) = \cos x, \cos (\pi / 2 - \alpha) = \sin \alpha and \tan \alpha = \sin \alpha / \cos\alpha.
- \sin(\alpha+\beta) = \sin \alpha\cos \beta + \cos \alpha \sin \beta.
- \cos(\alpha+\beta) = \cos \alpha\cos \beta - \sin \alpha \sin \beta.
Then you can derive the following formulas:
- \sin 2\alpha = ?, \cos 2\alpha = ?, \tan (\alpha+\beta) = ?, \tan 2\alpha = ?.
- \sin \alpha - \sin \beta = ? (hint: let x=(\alpha+\beta)/2, y=(\alpha-\beta)/2), \cos \alpha - \cos \beta = ?.
- \sin\alpha\cos\beta = ? (hint: replace \beta by -\beta in 3 and add it to 3), \sin\alpha\sin\beta = ?, \cos\alpha\cos\beta = ?.