Method of Integrating Factors
An integrating factor is a function by which an ordinary differential equation can be multiplied in order to make it integrable.
Problem 1 Solve y' = 2y + 3e^x.
Solution The big idea of integrating factor is to multiply both sides of the DE y' - 2y = 3e^x by \mu(x) so that the left hand side becomes (\mu y)'. In other words, \mu ought to satisfy (\mu y)' = \mu y' - 2\mu y.
By the product rule, we get \mu y' + \mu' y = \mu y' - 2\mu y, which gives \mu' = -2\mu. The solution of the last DE is \mu(x) = e^{-2x}. Thus multiplying both side of y' - 2y = 3e^x by the integrating factor gives (e^{-2x}y)' = 3e^{-x}. Integrate the last equation, e^{-2x}y = -3e^{-x} + C, hence y = -3e^x + Ce^{2x}.
Remark In general, the integrating factor of y' + p(x)y = q(x) is \mu(x) = \exp \int p(x) dx.
Problem 2 Solve y' + \frac{1}{x} y = 3\cos 2x for x > 0.
Solution The integrating factor is \exp \int \frac{1}{x} dx = \exp \ln x = x. Multiplying both sides of the DE, we have (xy)' = 3x\cos 2x, and so xy = \int 3x\cos 2x dx. Using integration by parts, we get xy = \int 3x \cos 2x dx = \frac{3}{4}(2x\sin 2x+\cos 2x) + C, and so y = \frac{3}{4}(2\sin 2x + \frac{1}{x}\cos 2x) + \frac{C}{x}.
Separable Equations
A separable differential equation is an equation of the form a(x)dx=b(y)dy. Let A(x), B(y) be the anti-derivative of a(x), b(y). Then A(x) = B(y) + C for some constant C depending on the initial condition. In general, you can solve separable equations essentially by “separating the two variables x and y, and you can then usually solve for y in terms of x.
Problem 3 Solve dy/dx=x^2/y^2 with the initial condition y(0)=2.
Solution Separate the tow variables y^2dy = x^2dx. Integrate and get \frac{1}{3}y^3 = \frac{1}{3}x^3 + C, that is, y^3 = x^3 + C. Using the initial condition, C = 8.
Problem 4 Find the implicit solution of dy / dx = \frac{y-4x}{x-y}.
Solution We cannot directly separate the two variables. However, because the equation is a homogeneous differential equation, heuristically, the substitution v=y/x helps. Since y = vx, we have \frac{dy}{dx} = x \frac{dv}{dx} + v and \frac{y-4x}{x-y} = \frac{y/x-4}{1-y/x} = \frac{v-4}{1-v}. We write the DE of x and y as a DE of x and v: x \frac{dv}{dx} + v = \frac{v-4}{1-v} and so x\frac{dv}{dx} = \frac{v-4}{1-v}-v=\frac{v^2-4}{1-v}. Now separate the two variables \frac{1-v}{v^2-4}dv = \frac{dx}{x}. Integrate and get -\frac{1}{4}\ln |v-2|-\frac{3}{4}\ln |v+2| = \ln |x|, that is, \ln |v-2| + 3\ln |v+2| = -4\ln |x| + C. Exponentiation both sides gives (v-2)(v+2)^3=Ax^{-4}. Multiplying both sides by x^4 gives (vx-2x)(vx+2x)^3=A. Recall vx = y, we obtain (y-2x)(y+2x)^3=A.
Curve of fastest descent
Johann Bernoulli posed the problem of the brachistochrone to the readers of Acta Eruditorum in June, 1696. He said,
I, Johann Bernoulli, address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument. Following the example set by Pascal, Fermat, etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise…
and he wrote the problem statement as
Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time.
In 1697 Johann Bernoulli used Fermat’s principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration.
By the conservation of energy, the instantaneous speed v after falling a height y in a uniform gravitational field is given by v=\sqrt{2gy}.
Bernoulli noted that the Snell’s law (also known as the law of refraction) gives a constant of the motion for a beam of light in a medium of variable density: \sin\theta / v = 1 / v_m, where v_m is the constant and \theta represents the angle of the trajectory with respect to the vertical.
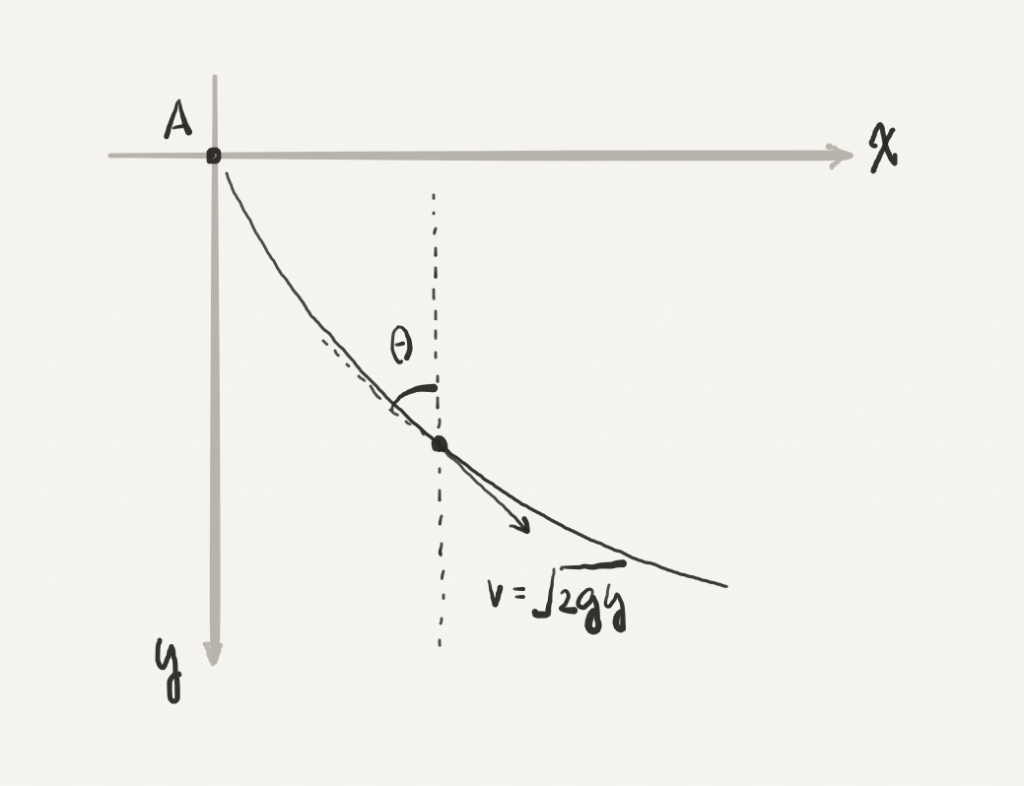
Problem 5 Show that the Brachistochrone curve is given by a function y = y(x) that satisfies the differential equation y' = \sqrt{k^2/y-1}, where k is a constant to be determined later.
Solution On one hand, the Snell’s law gives \sqrt{2gy} / \sin \theta = v_m, and so \sin \theta = \sqrt{y}/k for some constant k. On the other hand, \frac{dy}{dx} is the slope of the line tangent to the curve, and the slope is \frac{dy}{dx} = \cot \theta. Recall that \cot\theta = \frac{\sqrt{1-\sin^2\theta}}{\sin\theta}. We can eliminate \theta and get the desired DE.
The solution to the differential equation y' = \sqrt{k^2/y-1}, which describes a curve, is known as the cycloid. For more history on the problem of the brachistochrone, check the awesome video by 3Blue1Brown below.