Exact equations
Suppose we have the differential equation M(x,y)+N(x,y)y'=0 and a region D. If there is a function \Psi(x,y) so that \Psi_x(x,y) = M(x,y), \Psi_y = N(x,y) for all (x,y)\in D, then we call the differential equation exact in D. In this case, the implicit solution is \Psi(x,y) = c for (x,y)\in D, and we call \Psi(x,y) the potential function.
Theorem (Test for exact differential equation) Suppose the region D is simply connected. The differential equation M(x,y)+N(x,y)y'=0 is exact in D if and only if M_y(x,y) = N_x(x,y) at each (x,y)\in D.
Problem 1 Determine whether each of the equations is exact. If it is exact, find the solution. (a) 3x^2-2xy+2+(6y^2-x^2+3)y'=0; (b) (e^x\sin y-2y\sin x)+(e^x\cos y+2\cos x)y'=0.
Solution 1(a) Since \frac{\partial 3x^2-2xy+2}{\partial y} = -2x and \frac{\partial 6y^2-x^2+3}{\partial x} = -2x agree for all (x,y), the DE is exact. Let \Psi(x,y) be the potential function. Since \Psi_x = 3x^2 - 2xy + 2, \Psi = x^3 - x^2y + 2x + C(y). Since \Psi_y = -x^2 + C'(y) = 6y^2 - x^2 + 3, C(y) = 2y^3+3y. The implicit solution to the DE is then x^3-x^2y+2x+2y^3+3y = C.
Solution 1(b) Since \frac{\partial e^x\sin y - 2y\sin x}{\partial y} = e^x\cos y - 2\sin x and \frac{\partial e^x\cos y + 2\cos x}{\partial x} = e^x\cos y - 2\sin x agree for all (x,y), the DE is exact. Let \Psi(x,y) be the potential function. Since \Psi_x = e^x\sin y - 2y\sin x, \Psi = e^x\sin y + 2y\cos x + C(y). Since \Psi_y = e^x\cos y + 2\cos x + C'(y) = e^x\cos y + 2\cos x, C(y) = 0. The implicit solution to the DE is then e^x\sin y + 2y\cos x = C.
Idea It is sometimes possible to convert a differential equation that is not exact into an exact equation by multiplying the equation by a suitable integrating factor.
Problem 2 Given that the integrating factor depends on y only, solve y+(2x-ye^y)y'=0.
Solution Let \mu(y) be the integrating factor such that \mu(y)y+\mu(y)(2x-ye^y)y'=0 becomes exact. By the test for exactness, (\mu(y)y)_y = (\mu(y)(2x-ye^y))_x, equivalently, \mu'(y)y + \mu(y) = 2\mu(y). Thus \mu(y) satisfies \mu' = y\mu(y) and so \mu(y) = y. Therefore y^2 + (2xy - y^2e^y)y'=0 is exact. Let \Psi be the potential function. Since \Psi_x = y^2, \Psi = xy^2 + C(y). Since \Psi_y = 2xy + C'(y) = 2xy - y^2e^y, C(y) = \int -y^2e^y dy = -e^y(y^2-2y+2). The solution to the DE is then xy^2 - e^y(y^2-2y+2) = C.
Remark In general, M and N have to satisfy certain condition so that M(x,y)+N(x,y)y'=0 has an integrating factor \mu that depends on y only. Let \mu(y) be an integrating factor. This means \mu(y)M(x,y) + \mu(y)N(x,y)y' = 0 is exact. Thus (\mu(y)M(x,y))_y = (\mu(y)N(x,y))_x. The left hand side equals \mu'M + \mu M_y, and the right hand side equals \mu N_x. This shows \mu' M + \mu M_y = \mu N_x, that is \mu' = \frac{N_x - M_y}{M} \mu. The condition for the existence of such \mu is that \frac{N_x - M_y}{M} depends only on y.
Orthogonal families of curves
Definition Consider two families of curves \mathcal{F} and \mathcal{G}. We say that they are orthogonal whenever any curve from \mathcal{F} intersects any curve from \mathcal{G}, and the two curves are orthogonal at the point of intersection.
Example The families y = kx and x^2+y^2=r^2 are orthogonal.
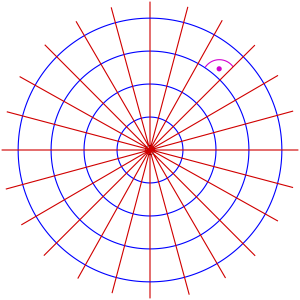
Question Given a family of curves \mathcal{F}, is it possible to find a family of curves which is orthogonal to \mathcal{F}?
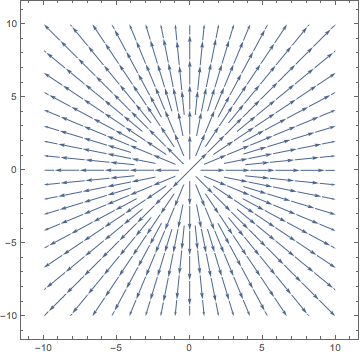
Example Each line through the origin, that is, y = ax, we have y' = a, and so xy' = ax = y. In other words, every line in the given family satisfies the DE xy' = y. Rewrite the DE as y' = y/x. The slope diagram is as follows:
Imagine that each little segment in the slope diagram turns 90 degrees:
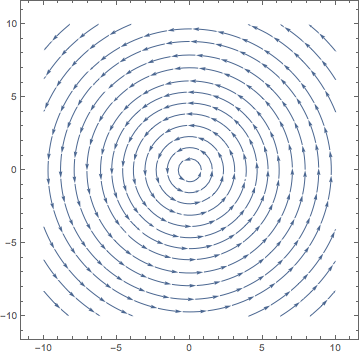
On one hand, the 2nd slope diagram satisfies the DE y' = -1/(y/x) = -x/y (why?). On the other hand, a solution (an integral curve) to the 2nd slope will intersect every line through the origin at a right angle (again, why?). This means the family of curves that is orthogonal to the family of lines through the origin satisfies the DE y' = -x/y. By separation of variables, x + yy' = 0, and so x^2+y^2 = C. This represents the family of circles centered at the origin.
We summarize the above discussion as follows.
Step 1 Find the differential equation associated to the given family of curves \mathcal{F} and rewrite this differential equation in the explicit form \frac{dy}{dx} = f(x,y).
Step 2 Write down the differential equation \frac{dy}{dx} = \frac{-1}{f(x,y)} associated to the orthogonal family \mathcal{G}, and solve the differential equation.
Optional step Give a geometric view of the two families.
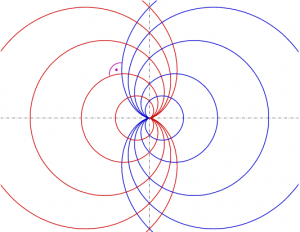
Exercise 1 Find the orthogonal family of the family of circles x^2+y^2=2cx.
Exercise 2 (Hard) Find the orthogonal family of the family of cardiods x^2+y^2+ax=a\sqrt{x^2+y^2}.