Problem 1: Solve the system of equations:
\begin{aligned}x_1 + 2x_2 - x_3 &= 6 \\ 3x_1 + 8x_2 + 9x_3 &= 10 \\ 2x_1 - x_2 + 2x_3 &= -2 \end{aligned}Comment: Use Gaussian elimination on the associated augmented matrix.
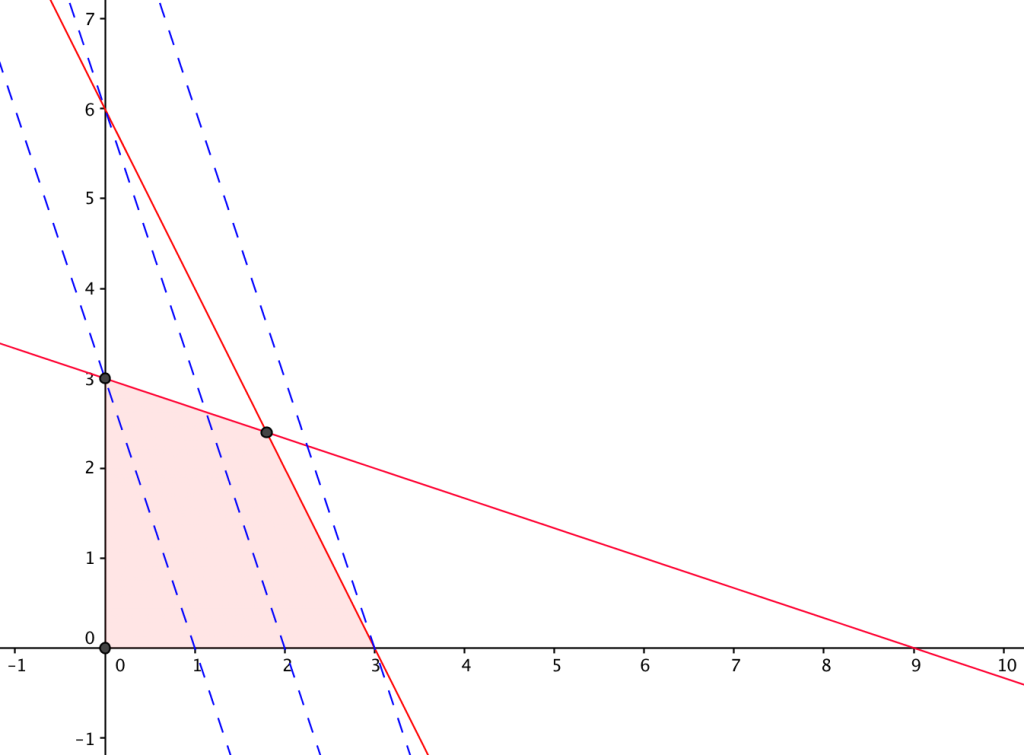
Problem 2: Solve graphically: maximize z = 3x_1 + x_2 subject to 2x_1 + x_3 \le 6, x_1 + 3x_2 \le 9, x_1 \ge 0, x_2 \ge 0.
Solution: The red lines are related to the first two constraints. The reddish area is the feasible domain. The dashed blue lines are level lines on which z=3,6,9 respectively. From the graph, z=9 is maximized by x_1 = 3, x_2 = 0.
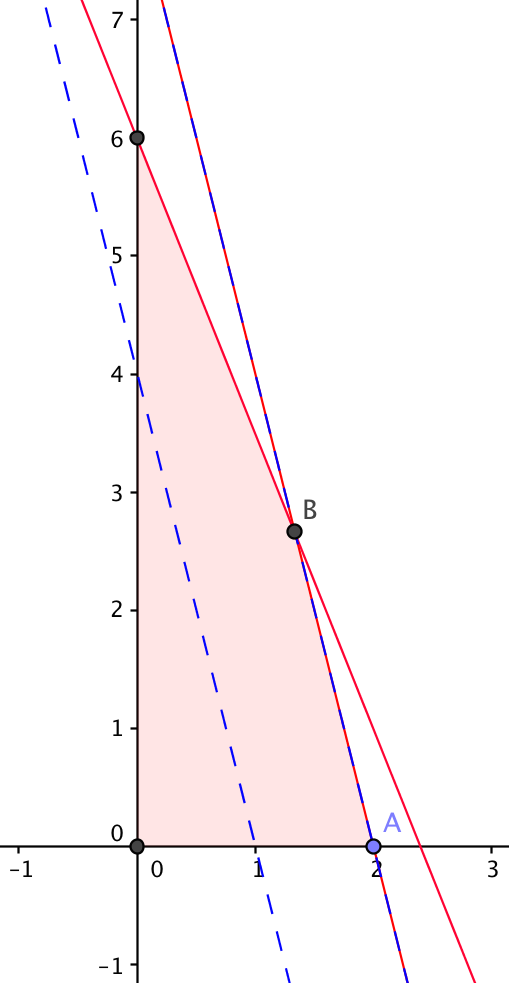
Problem 3: Solve graphically (should have non-unique solutions): maximize z=4x_1 + x_2 subject to 8x_1 + 2x_2 \le 16, 5x_1 + 2x_2 \le 12, x_1 \ge 0, x_2 \ge 0.
Solution: The red lines are related to the first two constraints. The reddish area is the feasible domain. The dashed blue lines are level lines on which z=4,8 respectively. From the graph, z=8 is maximized by points between A and B.
Problem 4: (A knapsack example) NASA must make a decision regarding which experiments should be flown on a deep-space probe that can accommodate a total payload of 140 pounds. A panel of experts has assigned numerical values to each of the experiments. The assigned values and the weights of the experiments are shown in the table. Formulate the linear programming problem that determines which experiments should be selected for the probe in order to achieve the greatest total value.
| Experiment | Weight | Value |
|---|---|---|
| 1 | 35 | 60 |
| 2 | 45 | 70 |
| 3 | 55 | 80 |
| 4 | 42 | 90 |
| 5 | 35 | 50 |
Solution: We want to maximize the total value 60x_1 + 70x_2 + 80x_3 + 90x_4 + 50x_5, where x_i is a variable that can assume only a 1 or a 0 depending on whether or not the item is on the probe. Those variables are subject to the total payload of 140 pounds, that is, 35x_1 + 45x_2 + 55x_3 + 42x_4 + 35x_5 \le 140.