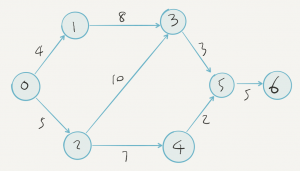
Example: Consider the CPM project network in the figure, where time is measured in days.
| Activity | Usual time | Crash time | Cost per day |
|---|---|---|---|
| (0,1) | 4 | 2 | $500 |
| (2,3) | 10 | 6 | $700 |
| (2,4) | 7 | 4 | $600 |
| (5,6) | 5 | 3 | $300 |
- Meeting a project deadline: If the durations on the edges of the network are the usual times, and the crash times and the costs of a day’s reduction for four of the activities are given in the table, set up a linear program to determine how to reduce the length of the project to 19 days as cheaply as possible.
- Minimizing total project cost: If there is a fixed cost involved with the project of $1,000 a day, set up the LP to minimize total project cost.
- Staying within budget: If a budget of $3,000 is available for reduction in time, set up the LP to determine the shortest time.
Solution: Let t_0, t_1, \dots, t_6 indicate the time of the event of the nodes, and let t_{01}, t_{23}, t_{24}, t_{56} indicate the time of the required to complete activity (0,1), (2,3), (2,4), (5,6).
Meeting a project deadline:
| Minimize | 500(4-t_{01}) + 700(10-t_{23})+600(7-t_{24})+300(5-t_{56}) |
|---|---|
| Subject to | t_1 - t_0 \ge t_{01} |
| t_2 - t_0 \ge 5 | |
| t_3 - t_1 \ge 8 | |
| t_3 - t_2 \ge t_{23} | |
| t_4 - t_2 \ge t_{24} | |
| t_5 - t_3 \ge 3 | |
| t_5 - t_4 \ge 2 | |
| t_6 - t_5 \ge t_{56} | |
| 4 \ge t_{01} \ge 2 | |
| 10 \ge t_{23} \ge 6 | |
| 7 \ge t_{24} \ge 4 | |
| 5 \ge t_{56} \ge 3 | |
| t_{6} - t_0 \le 19 |
Minimizing total project cost:
| Minimize | 500(4-t_{01}) + 700(10-t_{23})+600(7-t_{24})+300(5-t_{56})+1000(t_6-t_0) |
|---|---|
| Subject to | t_1 - t_0 \ge t_{01} |
| t_2 - t_0 \ge 5 | |
| t_3 - t_1 \ge 8 | |
| t_3 - t_2 \ge t_{23} | |
| t_4 - t_2 \ge t_{24} | |
| t_5 - t_3 \ge 3 | |
| t_5 - t_4 \ge 2 | |
| t_6 - t_5 \ge t_{56} | |
| 4 \ge t_{01} \ge 2 | |
| 10 \ge t_{23} \ge 6 | |
| 7 \ge t_{24} \ge 4 | |
| 5 \ge t_{56} \ge 3 |
Staying within budget:
| Minimize | t_6-t_0 |
|---|---|
| Subject to | t_1 - t_0 \ge t_{01} |
| t_2 - t_0 \ge 5 | |
| t_3 - t_1 \ge 8 | |
| t_3 - t_2 \ge t_{23} | |
| t_4 - t_2 \ge t_{24} | |
| t_5 - t_3 \ge 3 | |
| t_5 - t_4 \ge 2 | |
| t_6 - t_5 \ge t_{56} | |
| 4 \ge t_{01} \ge 2 | |
| 10 \ge t_{23} \ge 6 | |
| 7 \ge t_{24} \ge 4 | |
| 5 \ge t_{56} \ge 3 | |
| 500(4-t_{01}) + 700(10-t_{23})+600(7-t_{24})+300(5-t_{56})\le 3000 |