A Short Proof of the Nash-Williams' Partition Theorem

Notations.

1. \mathbb{N} – the set of natural numbers;
2. \binom{M}{k} – the family of all subsets of M of size k;
3. \binom{M}{<\omega} – the family of all finite subsets of M;
4. \binom{M}{\omega} – the family of all infinite subsets of M;

The infinite Ramsey theorem, in its simplest form, states that for every partition \binom{\mathbb{N}}{k} = \mathcal{F}_1 \sqcup \dots \sqcup \mathcal{F}_r, there exists an infinite set M\subset \mathbb{N} such that \binom{M}{k}\subset \mathcal{F}_i for some i\in [r]. The Nash-Williams‘ partition theorem can be seen as a strengthening of the infinite Ramsey theorem, which considers a partition of a subset of \binom{\mathbb{N}}{<\omega}.

Notations.

1. \mathcal{F}\restriction M – \mathcal{F}\cap 2^M, that is, the set \{s\in\mathcal{F} : s\subset M\}.
2. s \sqsubset t , where s,t are subsets of \mathbb{N} – s is an initial segment of t, that is s = \{n\in t : n \le \max s\}.

Definition. Let set \mathcal{F} \subset \binom{\mathbb{N}}{<\omega}.

1. \mathcal{F} is Ramsey if for every partition \mathcal{F}=\mathcal{F}_1\sqcup \dots\sqcup\mathcal{F}_r and every M\in\binom{\mathbb{N}}{\omega}, there is N\in\binom{M}{\omega} such that \mathcal{F}_i\restriction N = \emptyset for all but at most one i\in[r].
2. \mathcal{F} is a Nash-Williams family if for all s, t\in\mathcal{F}, s\sqsubset t \implies s = t.

Theorem (Nash-Williams 1965). Every Nash-Williams family is Ramsey.

The proof presented here is based on the proof given by Prof. James Cummings in his Infinite Ramsey Theory class. The purpose of this rewrite is to have a proof that resembles the one of the infinite Ramsey theorem.

Notation. Let s\in\binom{\mathbb{N}}{<\omega} and M\in\binom{\mathbb{N}}{\omega}. Denote $$[s, M] = \left\{t \in \binom{\mathbb{N}}{<\omega} : t \sqsubset s \text{ or } (s \sqsubset t \text{ and } t\setminus s \subset M)\right\}.$$

Definition. Fix \mathcal{F}\subset \binom{\mathbb{N}}{<\omega} and s\in \binom{\mathbb{N}}{<\omega}.

1. M accepts s if [s, M]\cap \mathcal{F}\neq \emptyset and M rejects s otherwise;
2. M strongly accepts s if every infinite subset of M accepts s;
3. M decides s if M either rejects s or strongly accepts it.

We list some properties that encapsulates the combinatorial characteristics of the definitions above.

Properties.

1. If M decides (or strongly accepts, or rejects) s and N\subset M, then N decides (respectively strongly accepts, rejects) s as well.
2. For every M\in\binom{\mathbb{N}}{\omega} and s\in\binom{\mathbb{N}}{<\omega}, there is N_1\in\binom{M}{\omega} deciding s. Consequently, there is N_2\in\binom{M}{\omega} deciding every subset of s.

Proof of Theorem. Enough to show that if \mathcal{F} = \mathcal{F}_1\sqcup \mathcal{F}_2, then for every M\in\binom{\mathbb{N}}{\omega}, there is infinite N\in \binom{M}{\omega} such that F_i \restriction N = \emptyset for some i\in[2].

We are going to use \mathcal{F}_1 instead of \mathcal{F} in the definitions of “accept”, “reject”, “strongly accept” and “decide”. Find N\in \binom{M}{\omega} that decides \emptyset. If N rejects \emptyset, by definition \mathcal{F}_1\restriction N = [\emptyset, N]\cap \mathcal{F}_1 = \emptyset. Otherwise N strongly accepts \emptyset.

Inductively, we build a decreasing sequence of infinite sets N \supset N_1 \supset N_2\supset \dots , an increasing sequence of natural numbers n_1, n_2, \dots, and maintain that n_i\in N_i, n_i < \min N_{i+1} and that N_i strongly accepts every s\subset \{n_j : j < i\}. Initially, we take N_1 = N as N strongly accepts \emptyset.

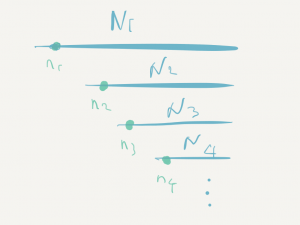
Suppose N_1 \supset \dots \supset N_i and n_1 < \dots < n_{i-1} have been constructed. In the following lemma, when taking M = N_i and s = \{n_j : j < i\}, it spits out m and N, which are exactly what we need for n_i and N_{i+1} to finish the inductive step.

Lemma. Suppose M\in\binom{\mathbb{N}}{\omega}, s\in\binom{\mathbb{N}}{<\omega} and \max s < \min M. If M strongly accepts every subset of s, then there are m \in M and N \in \binom{M}{\omega} such that n < \min N and N strongly accepts every subset of s\cup \{n\}

Proof of lemma. We can build M = M_0 \supset M_1\supset M_2 \supset \dots such that for every i, m_i := \min M_i < \min M_{i+1} and M_{i+1} decides every subset of s\cup \{m_i\}. It might happen that M_{i+1} rejects a subset of s\cup \{m_i\}. However, we claim that this cannot happen for infinitely many times.

Otherwise, by the pigeonhole principle, there is t\subset s such that I = \{i : M_{i+1} \text{ rejects }t\cup\{m_{i}\}\} is infinite. Let M' = \{m_i : i\in I\}. Note that [t, M'] \subset \cup_i [t\cup\{m_i\}, M_{i+1}], and so [t,M']\cap \mathcal{F}_1\subset \cup_i \left([t\cup\{m_i\}, M_{i+1}]\cap\mathcal{F}_1\right) = \emptyset. Hence M'\subset M rejects t\subset s, which is a contradiction.

Now we pick one i such that M_{i+1} strongly accepts every subset of s\cup\{m_i\}, and it is easy to check that m = m_i and N = M_{i+1} suffice. [qed]

Finally, we take N_\infty = \{n_1, n_2, \dots\}. For any s\in\binom{N_\infty}{<\omega}, there is i such that s\subset \{n_1, \dots, n_{i-1}\}. Note that N_i strongly accepts s and N_\infty\subset N_i. Therefore N_\infty (strongly) accepts s, that is [s, N_\infty]\cap \mathcal{F}_1 \neq \emptyset, and say t\in [s, N_\infty]\cap \mathcal{F}_1. Because t\in\mathcal{F}_1 and \mathcal{F} = \mathcal{F}_1 \sqcup \mathcal{F}_2 is a Nash-Williams family, s\notin \mathcal{F}_2. [qed]