Example 1: Evaluate \int_0^3\frac{dx}{x-1} if possible.
Hint: Because x=1 is the vertical asymptote of the integrant, we have to break the integral into \int_0^1\frac{dx}{x-1}+\int_1^3\frac{dx}{x-1}. The first integral is divergent.
Example 2: Determine whether \int_1^\infty\frac{\ln x}{x}dx is convergent or divergent.
Hint: Consider \lim_{t\to\infty}\int_1^\infty\frac{\ln x}{x}dx.
Problem 3: Determine whether \int_{-2}^{14}\frac{dx}{\sqrt[4]{x+2}} is convergent or divergent.
Hint: Consider \lim_{t\to -2^+}\int_t^{14}\frac{dx}{\sqrt[4]{x+4}}.
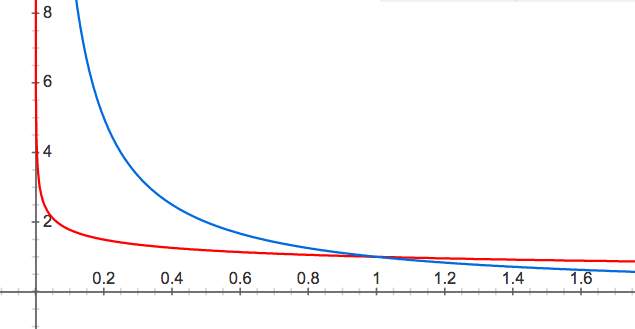
Remark: Here is a comparison picture of graphs of f(x)=1/x(blue) and g(x)=1/\sqrt[4]{x}(red). The `vertical tail’ of g is way thinner than f. This explains partly why \int_0^1f(x)dx is divergent whereas \int_0^1g(x)dx is convergent.
Example 4: Use the comparison theorem to determine whether \int_0^\infty\frac{x}{x^3+1}dx is convergent or divergent.
Hint: Break the integral into \left(\int_0^1+\int_1^\infty\right)\frac{x}{x^3+1}dx. The second integral converges because the integral is less than \frac{1}{x^2} for all x\geq 1.
Problem 5: Use the comparison theorem to determine whether \int_1^\infty\frac{x+1}{\sqrt{x^4-x}}dx is convergent or divergent.
Hint: The integral diverges because the integrand is greater than \frac{1}{x} for all x\geq 1.
Problem 6: Use the comparison theorem to determine whether \int_0^\infty\frac{\arctan x}{2+e^x}dx is convergent or divergent.
Hint: The integral converges because the integrand is less than \frac{\pi}{2}e^{-x} for all x\geq 0.
Problem 7: Use the comparison theorem to determine whether \int_0^1\frac{\sec^2x}{x\sqrt{x}}dx is convergent or divergent.
Hint: The integral diverges because the integrand is greater than or equal to 1/x\sqrt{x} for all 0\leq x\leq 1.