Example 1: The curve traced out by a point P on the circumference of a circle as the circle rolls along a straight line is called a cycloid. If the circle has radius r and rolls along the x-axis and if one position of P is the origin, find parametric equations for the cycloid.
Hint: Choose as parameter the angle of rotation \theta of the circle.
Definition: The curve is concave up when d^2y/dx^2>0 and concave down
when d^2y/dx^2<0.
Example 2: Find dy/dx and d^2 y/dx^2 for x=t^2+1, y=t^2+t. For which values of t is the curve concave upward?
Hint: Use dy/dx = (dy/dt)/(dx/dt) and d^2y/dx^2 = \frac{d(dy/dx)/dt}{dx/dt}.
Example 3: Graph the curve x=\cos t+2\cos2t,y=\sin t+2\sin2t to discover where it crosses itself. Then find equations of both tangents at that point.
Solution: The curve crosses itself at (-2, 0).
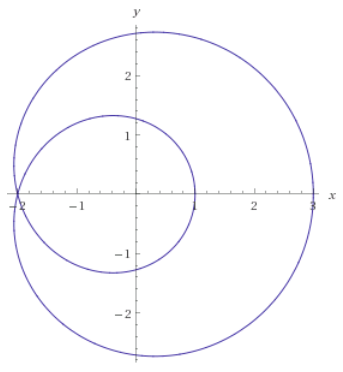
This happens when x = \cos t + 2 \cos 2t = \cos t(1+ 4\cos t)-2 = -2, y = \sin t + 2\sin 2t = \sin t(1+4\cos t) = 0, i.e., \cos t = -1/4. The tangent line at (x_0, y_0) where x_0 = x(t_0), y_0 = y(t_0) is given by y'(t_0)(x-x_0) = x'(t_0)(y-y_0), i.e., (\cos t_0 + 4\cos 2t_0)(x - x_0) = (-\sin t_0 - 4\sin 2t_0)(y - y_0). Now set \cos t_0 = -1/4, \sin t_0 = \pm\sqrt{15}/4, x_0 = -2, y_0 = 0 and get two equations of both tangents \sqrt{15}(x+2)\pm y=0.
Example 4: Use the parametric equations of an ellipse, x = a \cos \theta,
y=b\sin\theta,0\leq\theta\leq2\pi, to find the area that it encloses.
Solution: Suppose x=f(t) and y=g(t). Notice that as \theta increases, dx is negative and y is positive when 0 < \theta < \pi, and then dx positive and y negative when \pi < \theta < 2\pi. Therefore A=\int_0^{2\pi}g(t)f'(t)(-dt)=\int_0^{2\pi}b\sin\theta a\sin\theta d\theta=\pi ab.
Example 5: Find the exact length of the curve x=1+3t^2, y=4+2t^3, 0\leq t\leq 1.
Solution: The length of the curve is \int_0^1\sqrt{(6t)^2+(6t^2)^2}dt=4\sqrt{2}-2.
Example 6: Find the exact area of the surface obtained by rotating the given curve x=a\cos^3\theta, y=a\sin^3\theta, 0\leq \theta\leq\pi/2 about the x-axis.
Solution: The area of the surface is \int_0^{\pi/2} 2\pi a\sin^3\theta \sqrt{(3a\cos^2\theta\sin\theta)^2+(3a\sin^2\theta\cos\theta)^2}dt=\frac{6\pi}{5}a^2.