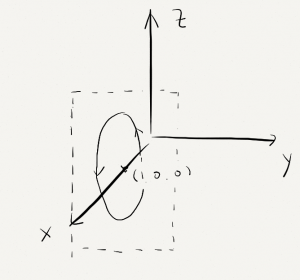
Section 10.7 Problem 9: Sketch the curve with the given vector equation. Indicate with an arrow the direction in which t increases. \mathbf{r}(t)=\langle 1, \cos t, 2 \sin t\rangle.
Solution: Since x(t) is always 1, the curve lies on the plane of x=1. Now let’s focus on this plane. On this plane, since \sin^2 t+\cos^2t=1, we have y^2+\left(\frac{z}{2}\right)^2=1. This is So we have the following picture on the plane of x=1.
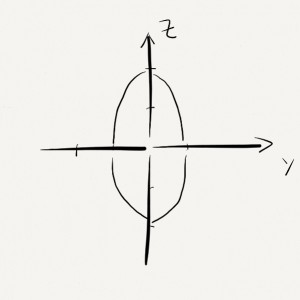
In order to find the the direction, we can let t=0, \frac{\pi}{2}, \pi etc. You will see the point moving clockwise.
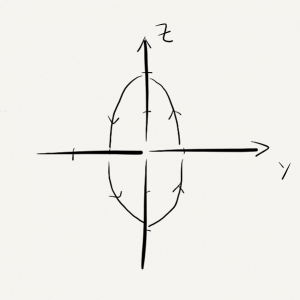
Finally, we assemble the plane of x=1 into the 3-d space.
Section 10.7 Problem 24: Show that the curve with parametric equations x = \sin t, y = \cos t, z = \sin^2t is the curve of intersection of the surfaces z=x^2 and x^2 +y^2 =1. Use this fact to help sketch the curve.
Partial solution: For any point on the curve, we know there is some t such that x=\sin t, y=\cos t, z=\sin^2 t. Hence z=\sin^2t=x^2 and x^2+y^2=\sin^2t+\cos^2t=1. So the curve is contained in the intersection of the surfaces.
On the other hand, for any point (x,y,z) satisfying both equations of the surfaces z=x^2 and x^2+y^2=1. As x^2+y^2=1, there is some parameter t such that x = \sin t, y = \cos t. Since z=x^2, we know z=\sin^2t. So the intersection of the surfaces is also contained in the curve.
The two way containment shows that the curve is exactly the intersection of the surfaces. Given this piece of information, to sketch the curve, we can just sketch both two surfaces and find the intersection.
Section 10.7 Problem 28: Find a vector function that represents the curve of intersection of the two surfaces. The cylinder x^2 +y^2 =4 and the surface z=xy.
Solution: From the first equation, we can parametrize x and y by x=2\cos t, y=2\sin t. By the second equation, z=xy=4\cos t\sin t=2\sin(2t).
Section 10.7 Problem 63: Evaluate the integral. \int \left(\sec^2t\mathbf{i}+t(t^2+1)^3\mathbf{j}+t^2\ln t\mathbf{k}\right)dt.
Comment: To find the integral of a vector function is equivalent to find the integral of each coordinate. Since this is an indefinite integral, your answer should involve a constant. In this problem the constant is not a constant number but a constant vector.
Section 10.7 Problem 67: If two objects travel through space along two different curves, it’s often important to know whether they will collide. (Will a missile hit its moving target? Will two aircraft collide?) The curves might intersect, but we need to know whether the objects are in the same position at the same time. Suppose the trajectories of two particles are given by the vector functions $$\mathbf{r}_1(t)=\langle t^2, 7t – 12, t^2\rangle, \mathbf{r}_2(t)= \langle 4t – 3, t^2, 5t – 6\rangle $$ for t \geq 0. Do the particles collide?
Solution: A collision means for some time t, \mathbf{r}_1(t)=\mathbf{r}_2(t). Thus t^2=4t-3, 7t-12=t^2, t^2=5t-6. Solve all three quadratic equations, there is only one common solution, which is t=3. Hence the particles collide at t=3.
Section 10.7 Problem 81: If \mathbf{r}(t) \neq 0, show that \frac{d}{dt} |\mathbf{r}(t)|=\frac{ 1}{|\mathbf{r}(t)|}\mathbf{ r}(t)\cdot \mathbf{r}'(t).
Sketch of Proof: The punchline is to take the derivative on the identity |\mathbf{r}(t)|^2=\mathbf{r}(t)\cdot \mathbf{r}(t). For the derivative of the left hand side, we use the chain rule and get 2|\mathbf{r}(t)|\frac{d|\mathbf{r}(t)|}{dt}. And for the derivative of the right hand side, we use the derivative rule for dot product and get \mathbf{r}'(t)\cdot \mathbf{r}(t)+\mathbf{r}(t)\cdot \mathbf{r}'(t)=2\mathbf{r}(t)\cdot \mathbf{r}'(t).
Section 10.8 Problem 7: Let C be the curve of intersection of the parabolic cylinder x^2 = 2y and the surface 3z = xy. Find the exact length of C from the origin to the point (6, 18, 36).
Solution: Let x=t. Since x^2=2y, y=t^2/2. Furthermore, since 3z=xy, z=xy/3=t^3/6. At t=0, the point is at origin and at t=6, the point is at (6, 18, 36). Now the vector function ]\mathbf{r}(t)=\langle t, t^2/2, t^3/6\rangle. Take the derivative and get ]\mathbf{r}'(t)=\langle 1, t, t^2/2\rangle. Hence |]\mathbf{r}'(t)|=\sqrt{1+t^2+t^4/4}=1+t^2/2 the exact length of C from the origin to the point (6, 18, 36) is equal to \int_0^6 (1+t^2/2)dt=42.
Section 10.8 Problem 11: Suppose you start at the point (0, 0, 3) and move 5 units along the curve x = 3 \sin t, y = 4t, z = 3 \cos t in the positive direction. Where are you now?
Solution: The vector function \mathbf{r}(t)=\langle 3 \sin t, 4t, 3 \cos t\rangle and \mathbf{r}(t)=\langle 3 \cos t, 4, -3 \sin t\rangle. Since \mathbf{r}(0)=(0,0,3), we know we start at time t=0. To where where we are now after moving 5 units, we just need to know at which time we have moved 5 units. Let that time be T. We know 5=\int_0^T|\mathbf{r}(t)|dt=\int_0^T \sqrt{(3\cos t)^2+4^2+(-3\sin t)^2}dt=\int_0^T 5dt=5T. So T=1 and \mathbf{r}(T)=\langle 3 \sin 1, 4, 3 \cos 1\rangle.
Section 10.8 Problem 15: (a) Find the unit tangent and unit normal vectors \mathbf{T}(t) and \mathbf{N}(t). (b) Use \kappa(t)=\frac{\mathbf{|T}'(t)|}{|\mathbf{r}'(t)|} to find the curvature. \mathbf{r}(t)=\langle \sqrt{2}t,e^t,e^{-t}\rangle.
Solution: (a) Since \mathbf{r}(t)=\langle \sqrt{2}t,e^t,e^{-t}\rangle, \mathbf{r}'(t)=\langle \sqrt{2},e^t,-e^{-t}\rangle and |\mathbf{r}'(t)|=\sqrt{2+(e^t)^2+(e^{-t})^2}=e^t+e^{-t}. So \mathbf{T}(t)=\frac{\mathbf{r}'(t)}{|\mathbf{r}'(t)|}=\frac{\langle \sqrt{2},e^t,-e^{-t}\rangle}{e^t+e^{-t}}. Moreover, \mathbf{T}'(t)=\frac{\langle \sqrt{2},e^t,-e^{-t}\rangle}{e^t+e^{-t}}=\frac{2}{(e^t+e^{-t})^2}\langle \frac{e^t-e^{-t}}{-\sqrt{2}}, 1, 1\rangle and |\mathbf{T}'(t)|=\frac{\sqrt{2}}{e^t+e^{-t}}. So \mathbf{N}(t)=\frac{\mathbf{T}'(t)}{|\mathbf{T}'(t)|}=\frac{\sqrt{2}}{e^t+e^{-t}}\langle \frac{e^t-e^{-t}}{-\sqrt{2}}, 1, 1\rangle. (b) \kappa(t)=\frac{\mathbf{|T}'(t)|}{|\mathbf{r}'(t)|}=\frac{\sqrt{2}}{(e^t+e^{-t})^2}
Section 10.8 Problem 17: Use \kappa(t)=\frac{|\mathbf{r}'(t)\times \mathbf{r}''(t)|}{|\mathbf{r}'(t)|^3} to find the curvature. \mathbf{r}(t)=t^3\mathbf{j}+t^2\mathbf{k}.
Solution: Since \mathbf{r}(t)=t^3\mathbf{j}+t^2\mathbf{k}, \mathbf{r}'(t)=3t^2\mathbf{j}+2t\mathbf{k} and \mathbf{r}''(t)=6t\mathbf{j}+2\mathbf{k}. Hence \mathbf{r}'(t)\times \mathbf{r}''(t)=(3t^2\mathbf{j}+2t\mathbf{k})\times 6t\mathbf{j}+2\mathbf{k}=-6t^2\mathbf{i}. Hence |\mathbf{r}'(t)\times \mathbf{r}''(t)|=6t^2 and |\mathbf{r}'(t)|=\sqrt{9t^4+4t^2}. So \kappa(t)=\frac{6}{(9t^2+4\sqrt{9t^4+4t^2}}.
Comment: We have two formulas for the curvature. The one used in problem 17 is easy to use than the one in problem 15 if we are only interested in finding curvature.